前面从理论上了解了下梯度学习算法的原理实现(如果没看的话建议先看下我前面写的原理实现点击此处跳转)，现在我们基于代码来实现预测房价，房价数据集仍是开源的波斯顿房价数据集，前面我们计算的公式如下

而O_0和O_1(图中的符号不好打，就这样表示了)迭代更新的公式为如下图 

其中图上标注的(1)和(3)都表示学习率，而(2)和(4)分别表示损失函数J对O_0求偏导和对O_1求偏导，写的有点不规范哈，偏导如何计算呢，因为J函数有2个变量，对某个变量求偏导，另一个变量看成函数而对这个变量直接求导即可，以下是我的求偏导过程

把上述求得的偏导数代入O_0和O_1迭代中的公式

公式到这里化简完了，接下来用代码实现，来看我们的目的，根据数据集进行训练来获得适合的O_0和O_1，这里学习率是有初始值的，自己设置即可(不要太大也不要太小)，而O_0和O_1最开始也要初始化一般设置较小值，为了好计算，本次使用numpy模块，将数据转化为二维数组(也叫矩阵)进行计算，代码如下

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import time
#设置防止中文乱码
plt.rcParams['font.sans-serif']=[u'SimHei']
plt.rcParams['axes.unicode_minus']=False
#载入数据，并进行读取
data = pd.read_csv('C:/users/14499/desktop/housing.data')
def notEmpty(s):
    return s!=''
#创建len(data)行，14列的空二维数组(矩阵)
df = np.empty((len(data), 14))
#迭代所有数据
for i, d in enumerate(data.values):
    #先使用filter去掉为空的字符串，然后将字符串分割成列表，并将列表元素转化为浮点型
    m = map(float, filter(notEmpty, d[0].split(' ')))
    #将这行数据存入二维数组的第i整行
    df[i] = list(m)
names = ['CRIM','ZN', 'INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
#设置列名，将原来的二维数组转化为代标签的二维数组，方便以列名进行存取
df1 = pd.DataFrame(df,columns=names)
#取房间个数数据
room_num = df1['RM']
#取价格数据
price_num = df1['MEDV']
print(room_num)
print(price_num)
#画房间数和价格的散点图
plt.figure()
plt.scatter(room_num,price_num,s=100,c='green',label="价格记录")
plt.title('房间数和房价关系')
plt.xlabel('房间数')
plt.ylabel('价格/(单位1000美元)')

#设置假设函数截距和斜率
O_0,O_1 = 0.01,10
#初始化参数
x = room_num
y = price_nu
#学习率
a = 0.0015
all_loss = []
print(np.random.randn())
for ii in range(100):
    #不断迭代O_0和O_1参数
    O_0 = O_0 - a*np.mean(O_0+O_1*x-y)
    O_1 = O_1 - a*np.mean((O_0+O_1*x-y)*x)
    Hx = O_0+O_1*x
    loss = np.mean(np.square(Hx-y))/2


    if ii%10 == 0:

        print("第{}次迭代的损失率为:{}-参数O_0为{} 参数O_1为{}".format(ii,loss,O_0,O_1))
    all_loss.append(loss)
plt.scatter(x,Hx,color='red',label="梯度下降法")
plt.legend(loc="upper left")
plt.show()

上面很详细的注释，很容易看懂，主要是损失率很少可能为0(特别是面对海量数据情况下)O_0和O_1也基本很少为0，因此·我们不知道什么时候迭代收敛，只能通过遍历的方式进行观察并调整，然后我们使用matplotlib来画出假设函数和原数据散点图的拟合程度，如图所示

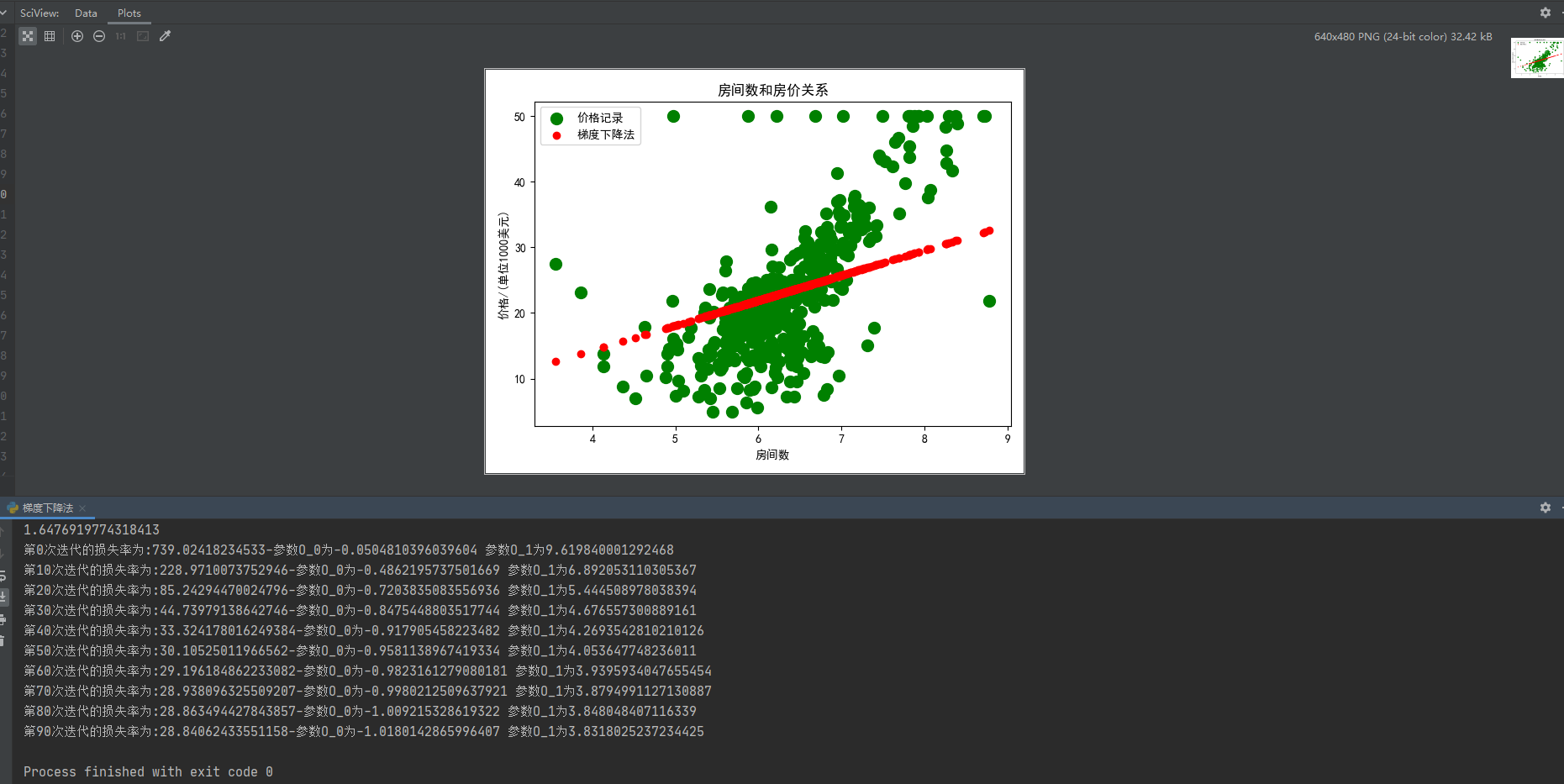
这里是每隔10的整数打印下输出，通过控制台的内容，很容易知道O_0和O_1分别为-1.01和3.831损失变化平缓，我们再来看下这10次假设函数(拟合函数)的变化过程，如图所示

从1一步一步拟合数据集。加行代码即可，加的以下第二行的代码

    if ii%10 == 0:
        plt.plot(x,Hx)
        print("第{}次迭代的损失率为:{}-参数O_0为{} 参数O_1为{}".format(ii,loss,O_0,O_1))

 

接下来我们看下损失值的变化情况，如图所示

在末尾加行代码

plt.plot(all_loss)
plt.xlabel("迭代次数",fontsize=14)
plt.ylabel("损失值",fontsize=14)
plt.show()

如果代码不懂的话可以仔细去了解下numpy库的基本使用，很容易上手的，以上是本人的学习过程，有点小问题莫怪哈